Fonction convexe Fonction qui est telle que $$\forall x,y,\forall t\in[0,1],\quad f(tx+(1-t)y)\leqslant tf(x)+(1-t)f(y)$$

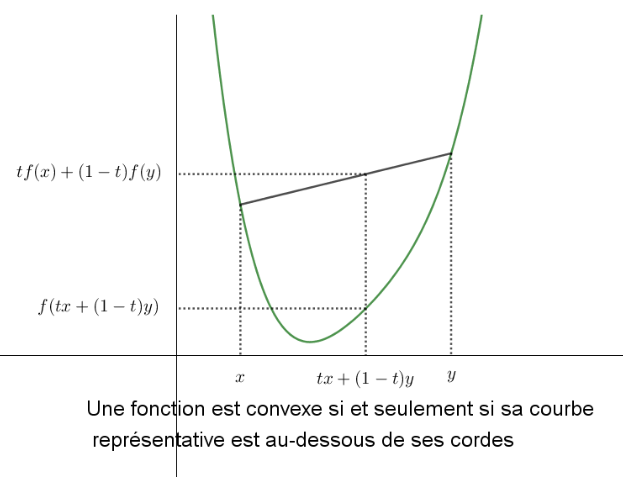
• on dit que la fonction est strictement convexe si l'inégalité est stricte
• on dit que la fonction est concave si l'inégalité est dans l'autre sens
• caractérisation pour les fonctions réelles deux fois dérivables : la dérivée seconde est positive
• caractérisation si \(f\) est différentiable : \(f(y)\geqslant f(x)+df(x)(y-x)\) (\(f\) est au-dessus de sa tangente)
• si \(f:C\subset E\to\;]-\infty,+\infty]\) est convexe, alors on peut la prolonger en \(\tilde f\) sur \(E\) en prenant \(\tilde f(x)=+\infty\) si \(x\notin C\) \(\to\) \(\tilde f\) est alors également convexe
• les Minimum locaux d'une fonction convexe sont en fait des minimum globaux
    
• si la convexité est stricte, alors on a existence et unicité du minimum global
    
• "Pour trouver le minimum d'une fonction convexe, il suffit de chercher un minimum local"

Questions de cours

START
Ω Basique (+inversé optionnel)
Recto: Que dire de la convexité de \(\exp\) sur \({\Bbb R}\) ?
Verso: Elle est convexe.
Bonus:
Carte inversée ?:
END
START
Ω Basique (+inversé optionnel)
Recto: Que dire de la convexité de \(x\mapsto x^n\) sur \({\Bbb R}\) ?
Verso:

• si \(n\) est pair, elle est convexe sur \({\Bbb R}\)
• si \(n\) est impair, elle est concave sur \({\Bbb R}_-\) et convexe sur \({\Bbb R}_+\)

Bonus:
Carte inversée ?:
END
START
Ω Basique (+inversé optionnel)
Recto: Que dire de la convexité de la fonction \(\lvert\cdot\rvert\) ?
Verso: Elle est convexe
Bonus:
Carte inversée ?:
END
START
Ω Basique (+inversé optionnel)
Recto: Que dire de la convexité de la fonction \(x\mapsto\sqrt x\) ?
Verso: Elle est concave sur \({\Bbb R}_+\)
Bonus:
Carte inversée ?:
END
START
Ω Basique (+inversé optionnel)
Recto: Quelles sont les fonctions à la fois convexes et concaves sur \({\Bbb R}\) ?
Verso: Ce sont les fonctions affines.
Bonus:
Carte inversée ?:
END
START
Ω Basique (+inversé optionnel)
Recto: Quand a-t-on le cas d'égalité dans l'inégalité d'une fonction convexe ?
$$\forall x,y,\forall t\in[0,1],\quad f(tx+(1-t)y)\leqslant tf(x)+(1-t)f(y)$$
Verso: \(f\) est affine ou \(x=y\).
Bonus:
Carte inversée ?:
END

Exercices

Montrer \((\implies)\) :

On a le résultat en prenant l'inégalité de convexité et en calculant la différentielle avec \(t\in[0,1]\).

Montrer \((\impliedby)\) :

On prend les inégalités en \(x\) et en \(y\) et on les multiplie et on les ajoute, ce qui nous donne l'inégaltié de convexité.

Montrer \((\implies)\) :

L'inégalité de convexité donne bien le caractère convexe de \(\operatorname{epi}(f)\).Q

Montrer \((\impliedby)\) :

Il faut utiliser le fait que les points du type \((x,f(x))\) sont dans \(\operatorname{epi}(f)\).

On utilise la question précédente.

On conclut en disant qu'une intersection de convexes est convexe.

Faire la première partie de la question.

Cela se fait rapidement par la méthode générale.

Faire la deuxième partie de la question.

On va raisonner par l'absurde.

L'inégalité de convexité stricte amène à une contradiction.

La question précédente nous donne l'existence.

En supposant par l'absurde que \(S\) ait \(\geqslant2\) éléments, on a une contradiction avec l'inégalité de convexité stricte.